GibbsLDA, free LDA implementation (Xuan-Hieu Phan, Tohoku University)
Text file processing and data preparation (Outputs data in format valid for GibbsLDA)
Latent Dirichlet Allocation
Latent Dirichlet Allocation (LDA) was introduced by David M. Blei and others in 2003. It is actually modification of PLSA that allows to use one more apriori information about the content of documents. We know that documents usually are dedicated to one or two topics, rarely more than two, so when PLSA returns result saying that particular document contains twenty evenly presented topics we know that this may be wrong but can only ignore the result and not modify it. LDA has additional control parameter (usually denoted as alpha), that can be used to narrow down the list of topics.The foundation of LDA concept is presumption that each document contains random sample of topics taken from multinomial Dirichlet distribution. I say presumption because authors did not prove that topics in large collections have Dirichlet distribution but only stated it. It actually does not matter how close real distribution of topics to Dirichlet distribution because many statistical applications work very well using very approximate models, such as using normal distribution, when actual data has sort of bell-shape distribution, that only remotely reminds normal distribution for someone who has vivid enough imagination. The multinomial distribution is coordinated distribution of several parameters at once (in this case topics or categories). On that reason it is not that simple to imagine it graphically or draw a chart like it is done for normal distribution. The formula for probability density is provided in every article about Dirichlet distribution, but it does not help to imagine it. For better undersanding I borrowed couple of images from very detailed article about Dirichlet distribution.
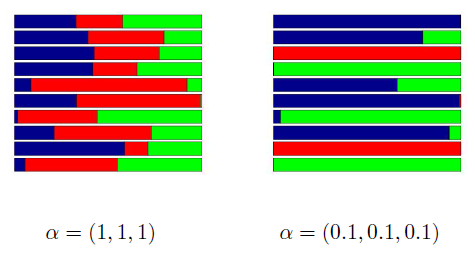
The article provides detailed explanation how to generate samples from Dirichlet distribution on example of breaking stick into pieces. In the pictures stick pieces are shown in the different colors. About same pictures can be drawn showing proportions of topics in documents. Note how parameter alpha affects the sizes of each fragment. Some more details about LDA can also be found in elementary introduction by Edwin Chen and fundamental explanation by David A. Blei. In applications for text categorization the parameters that define probability of each topic are equal and considered as single parameter that defines smoothness of the distribution of topics. Users can download open source example developed by Xuan-Hieu Phan from the top for a quick test. For explanation we may consider same tiny data set that is used in PLSA article of this site.
| doc/word | w1 | w2 | w3 | w4 | w5 |
| d1 | 8 | 2 | 2 | 0 | 0 |
| d2 | 9 | 1 | 1 | 0 | 0 |
| d3 | 0 | 1 | 2 | 1 | 7 |
| d4 | 0 | 1 | 2 | 1 | 8 |
The result of categorization by LDA is below
0.961538 0.038462 0.958333 0.041667 0.041667 0.958333 0.041667 0.958333 0.131915 0.727660 0.131915 0.004255 0.004255 0.182222 0.004444 0.093333 0.626667 0.093333The first table is doc/category, it clearly shows that top two documents and bottom two documents belong to different categories. The second table shows distribution of words in documents. It has great similarity with the same table of PLSA (columns have different order). The command line pass smoothness parameter (alpha), number of topics and name of the data file.
gibbslda.exe -est -alpha 0.5 -ntopics 2 -dfile data.txtThe data file needs to be in proper format
4 C C A B A A B A A A A A A A A A B C A A A A A E E B C C D E E E E E D C C E E E E E E B ENumber 4 shows number of documents. Each line represents space separated tokens sitting in every document, the symbols can be chosen arbitrarily, the order is unimportant. As you can see first line contains 8 symbols A, 2 symbols B and 2 symbols C, that match the first row of document/term table. Same format is used for other lines. Changing alpha from 0.5 to 5.0 returns different result for categories
0.681818 0.318182 0.714286 0.285714 0.333333 0.666667 0.333333 0.666667We can still see the correct categorization but the distribution of topics in each document is too smoothed. So alpha can be used to bring number of topics to apriori presumed number, which is the very important advantage of LDA, because few documents may be manually examined and alpha may be adjusted to better approach the expected result.
In order to process PATENTCORPUS128 collection, the document/term matrix should be reformatted into readable by GibbsLDA form. The application that process files and outputs data in format valid for further LDA can be downloaded from the link at the top. The categorization result is not very impressive. It varies each time but on average is about 45 percent of correct recognition. Actually, it is near PLSA.



