Elementary demo of tf-idf problem
C# implementation of HAC test
Elementary demo of HAC using training sample
Elementary demo of HAC for random samples from collection
Hierarchical Agglomerative Clustering
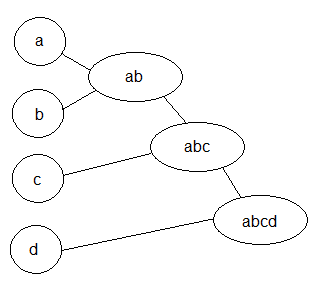
HAC is known since 1980th (Willett, 1988, Voorhees, 1986). The coding sample is about 300 lines long. The complexity or, being more precise, simplicity allows this code to be written by a student of computer school for one business day. Compared to Latent Semantic analysis (LSA) and Probabilistic Latent Semantic Analysis (PLSA) it shows significant advantage. For the same data sample the accuracy for LSA is about 62 percent, PLSA may provide an improvement if to start it from good initial approximation, but shows only 40 percent accuracy otherwise. HAC shows 84 percent accuracy. Besides accuracy, HAC does not need initial set of manually categorized files - i.e. human intervention.The matter of algorithm is merging closest couple of documents into one like it is shown in picture.
The proximity of two documents may be determined differently. There is no evidence that one particular method is better than others. The most common way is cosine similarity measured by a scalar computed as:
aTb / (||a|| * ||b||)
It is convenient because it filters the influence of the size of document. In my DEMO the computed cosine is adjusted for the number of merged documents. When merging two groups the result is divided by the size of the smaller group.
Updated on Mar. 16, 2012
The algorithm for building clusters is computationally optimized. After merging the clusters only those matrix elements that are affected by merging are recalculated. The speed is increased in several hundred times.Also tf-idf concept was researched. The result was surprising and unobvious. It showed that introduction of weight coefficients can make very little improvement, such as 3 percent, if weight coefficients are chosen correctly, but it can make significant deprovement otherwise. For the test sample the correct choice is known but for the real data it is presumed that lead to very high probability that natural word statistics will be destroyed and outcome deproved. It can be seen on the test program (the first link at the top). In order to run experiment the document-term matrix should be created by any of available programs including HAC (second link at the top). The tf-idf concept was tested by building another document-term matrix with corrected statistics. It is done in function
public bool makeCorrectedDocTermMatrix(string datafile, string datafile1)The function computes number of documents where each word was observed and introduce weight coefficients for so-called good words that means words that are observed in number of files that is close to cluster size. Users can experiment with the program by changing these weights sitting in array
int[] m_weightWhen all elements are equal to 1, the corrected document-term matrix is the same as original. It can be checked by binary comparison of files. When changing, let say, 17th element from 1 to 2, we double the frequency of every word that was observed in exactly 16 files (first element is ignored). So it is very easy to experiment. Amazingly, almost every change lead to deprovement and very few just slightly improve the result on a miserable percent.
HAC with training sample (added on Mar. 18, 2012)
When training sample is available we can use it in HAC algorithm in different ways. One of them is to check before merging two clusters if files within clusters belong to the same group known from training and simply allow or reject merge depending on the check. The example of such code is shown on the third link from the top. It presumes usage of document-term matrix built for PATENTCORPUS128. The technical details can be easy found in code. Originally we provide training data in the form of taboo list
private int[] m_nTabooList =
{ 0, -1, 0, 0, 0, -1, -1, 0, -1, 0, -1, 0, -1, -1, 0, -1,
-1, 1, -1, -1, 1, 1, 1, -1, -1, 1, 1, -1, -1, -1, 1, 1,
-1, 2, 2, -1, -1, 2, -1, 2, -1, -1, 2, 2, 2, 2, -1, -1,
-1, 3, -1, 3, -1, -1, 3, -1, 3, 3, -1, 3, 3, -1, 3, -1,
-1, -1, 4, 4, 4, -1, -1, 4, 4, -1, 4, -1, 4, -1, 4, -1,
-1, 5, 5, -1, -1, -1, 5, -1, -1, 5, 5, -1, 5, 5, 5, -1,
-1, 6, -1, -1, 6, 6, 6, 6, -1, 6, -1, -1, 6, -1, 6, -1,
7, 7, 7, -1, 7, -1, -1, -1, 7, -1, -1, 7, -1, 7, 7, -1};
It is a chart for every file in the list. Files to be categorized are assigned -1. Files with
known category are assigned different from -1 index. The size of data is 128 files and
the size of training sample is 64 (non negative elements). At the start we create
as many clusters as files we have, and each cluster gets the index from the above
list. When we merge we check indexes and allow merge only if one of them is
negative or both are equal. Otherwise we disallow merge and the next close
two clusters are considered. After the merge of two clusters, new cluster gets
the correspondent index. Obviously, this code works for both HAC with training sample and without it. When training sample is not available every element in above array is negative. The efficiency of this algorithm is not as good as I expected, however, it works. We can compare this example to Random Forest. The training sample is the same, but Random Forest showed accuracy about 65 percent while HAC with training sample showed 97 percent. Same data without training sample show 84 percent. The execution time for HAC with training data is much shorter. It is actually something near one second for this data.
Multi-level HAC with random sampling from collection (added on Mar. 20, 2012)
Large collections need multithreading and random sampling. The example of processing of such sample can be found at the fourth link from the top. In multi-processor systems random samples can be taken from collection and processed concurrently. The clusters returned from every thread can then be processed further for obtaining final result.


