Concept of Semantic Search
This section represents collection of reviews along with programs that can be downloaded and used to reproduce the result. This introductory article can be read by anyone, other articles need some math training on engineering level.There is one interesting legend about patent attorney who asked each inventor to draw his idea on the matchbox. When inventor complained on insufficient space, attorney answered that invention is not ready yet for patenting. It is true for very many concepts of semantic search. They can be drawn on matchboxes but can be understood by someone with bachelor degree in math. Another truth about semantic search may match another joke about one couple who was lost when riding car in town. When they stopped at the traffic light a woman, who was on the right seat, opened the window and asked man in the next car Where are we? He answered: You are in the car. She turned to a husband and said: He must be mathematician, the answer is precise but useless.
I found many semantic search concepts falling under this category: very interesting, impressive, but not very effective. Now I explain two concepts, that are proven to be effective, in matchbox format as for patent attorney, so people can understand how it is possible to find document not by the words it contains but by the meaning of what it says.
One concept is called Hierarchical Agglomerative Clustering. It is used to group documents in clusters according to what they say. On the first step document-term matrix is constructed. It is simply a table that contains numbers of how many times each word occurred in each document. For real data such matrices have sizes of 50 thousand words and 1 or 2 million documents. For our explanation we use 5 documents, 5 words and 2 presumed clusters, one is ROOM-DECORATION and another is COMPUTERS.
| Document/Term | PROCESSOR | SOFA | INTERFACE | TABLE | SOFTWARE |
| doc 1 | 1 | 0 | 0 | 0 | 1 |
| doc 2 | 3 | 0 | 0 | 0 | 1 |
| doc 3 | 0 | 0 | 1 | 0 | 1 |
| doc 4 | 0 | 4 | 0 | 2 | 0 |
| doc 5 | 0 | 1 | 0 | 5 | 0 |
After document-term matrix is constructed we combine two closest documents in one. This pair of closest documents can be identified by the best match in used words. The details how to do that may vary, but obviously in this case it is documents 4 and 5. After merging these two documents in one, our matrix is changed into following:
| Document/Term | PROCESSOR | SOFA | INTERFACE | TABLE | SOFTWARE |
| doc 1 | 1 | 0 | 0 | 0 | 1 |
| doc 2 | 3 | 0 | 0 | 0 | 1 |
| doc 3 | 0 | 0 | 1 | 0 | 1 |
| doc 4,5 | 0 | 5 | 0 | 7 | 0 |
Repeating the same step again will make first two documents to be merged in one:
| Document/Term | PROCESSOR | SOFA | INTERFACE | TABLE | SOFTWARE |
| doc 1,2 | 4 | 0 | 0 | 0 | 2 |
| doc 3 | 0 | 0 | 1 | 0 | 1 |
| doc 4,5 | 0 | 5 | 0 | 7 | 0 |
Next step is final we merge documents until its number becomes equal to number of sought categories. The document in the middle is closer to upper two than to lower two:
| Document/Term | PROCESSOR | SOFA | INTERFACE | TABLE | SOFTWARE |
| doc 1,2,3 | 4 | 0 | 1 | 0 | 3 |
| doc 4,5 | 0 | 5 | 0 | 7 | 0 |
Now what happen if we fire the query with word PROCESSOR against the original matrix? It returns document 1 and 2 but not 3 because document 3 does not contain word PROCESSOR. And what happen if we run same query against clusters? It returns first cluster that means documents 1,2 and 3, although document 3 does not contain word PROCESSOR, but it may speak about computers because it has word INTERFACE and this word is noticed being in the same document with word SOFTWARE and the latter is sitting next to PROCESSOR in some other document. Although this algorithm is very simple it is proven to be very effective as well and can be explained to a child. Imagine the child saying that they have learned today at school how to execute Semantic Document Search by applying Hierarchical Agglomerative Clustering.
HAC (Hierarchical Agglomerative Clustering) only reduce number of relevant documents from, let say, 2 million to, let say, 100,000, because it makes clusters and returns the relevant cluster. Obviously, it may miss some very important documents, it does not guarantee 100 percent accuracy and that is true for any other clustering technology. HAC can be improved and amended but we finish its explanation at this point and move on further.
The clustering may be considered as pre-selection process. The next step is to separate pre-selected documents into RELEVANT, IRRELEVANT classes. This task is more challenging than clustering. To understand the challenge I suggest to consider imaginary program that splits stream of messages into two classes GOOD NEWS, BAD NEWS. Imagine the program where you can type a message, hit a button and imaginary program answers either GOOD FOR YOU or I'M SO SORRY, for example:
I lost ten pounds. - GOOD FOR YOU
I lost my wallet. - I'M SO SORRY
My wife is on vacation. She is out of town with kids. - GOOD FOR YOU
and so on. This imaginary program should have human life experience in order to tell GOOD NEWS from BAD NEWS. Unfortunately, the algorithm that can function in wide generic format for every possible news is not yet discovered, but if we narrow the area to very specific subject, such as messages only about MONEY, it may be successful. For this last task we can use another proven very effective technique called Support Vector Machine (SVM), which is proposed by university professor Vladimir Vapnik, but it also can be explained in matchbox format. This part requires human intervention. Human reads several randomly selected documents and separates them into two groups: RELEVANT, IRRELEVANT. If vocabulary of our documents contains only 3 words (COMPUTER, INTERFACE, FLOOR) we can assign a unique point in 3D space for each document. After collecting of large group of such points we can separate them from each other by a plane.
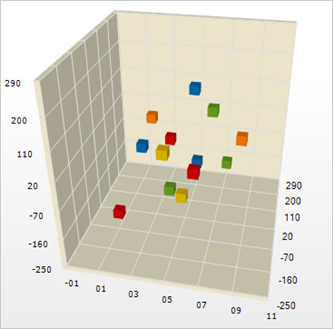
If such plane does not exist, the best possible solution is sought. The concept is the same for larger dictionaries and works in the same way in n-dimensional spaces by using hyperplanes. And considering details, it has to be said that hyperplanes not necessarily planes but can also be surfaces. But we limit our explanation to matchbox format. The process of separation of all documents within category into RELEVANT/IRRELEVANT classes is continued after training by indentifying on which side of hyperplane each document is located.
If we ask large number of people to provide phrases about MONEY carrying either GOOD NEWS or BAD NEWS, we shall be able to train computer to distinguish semantic using SVM. Obviously, if people try, they can fool algorithm but people don't have that objective when making documents, so the technology works with acceptable accuracy. This programmatic identification of GOOD NEWS and BAD NEWS may be seen as sort of brain exercise for designer, but if applied inside programmatic real-time news analyzer used for instant prediction of their influence on the stock prices, that can make such algorithm very practical and useful for some people. The other name for algorithms that split text fragments into only two categories GOOD and BAD is called sentiment analysis. It is used by large corporations to identify feelings of people regarding the goods that they produce. They, usually, use public networks and chat sites as data source.
The special case in semantic search is paraphrase identification, for example, following two e-mails
Read enclosed document and provide your opinion
Please look at attached file and tell me what you think
convey the same order but use completely different vocabulary. One very complicate approach to identify equivalence of these sentences is known. It is sort of translation of sentences into special logical language that looks like formulas and use limited vocabulary, and in this artificial language these phrases are identical. I see it as a dead end in semantic search. We know that all attempts to create languages failed. This problem can be solved like in automatic translation, i.e collect sentence couples and statistics on context word usage. For example, if I suggest to write more sentences with the same meaning but different words, how many of those can be added? Not many. That means we can have bank of paraphrases and use it for detecting of short semantic equivalents.
This is the end of our quick introduction into semantic search. The other topics in this research section are dedicated to evaluation of the efficiency of different known algorithms. The explanation, however is not in matchbox format, readers are presumed to have basic knowledge of mathematics.



