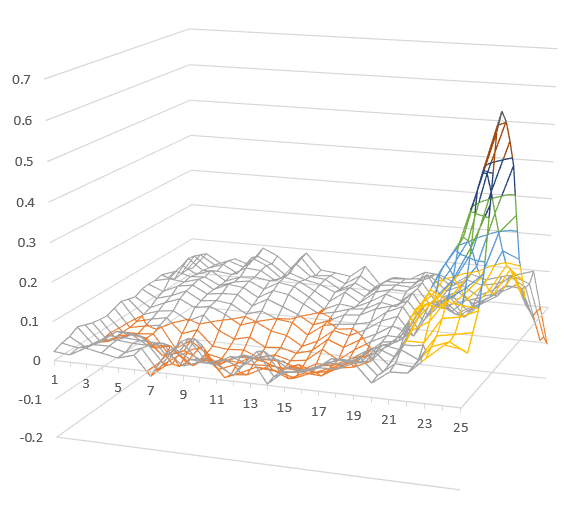
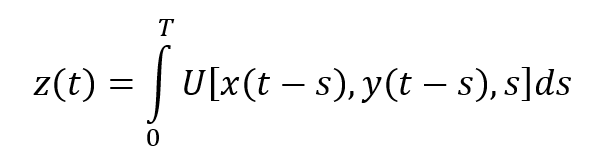Identification test on non-linear mechanical systems
Download of entire C# code along with the test data U-Test.zip
This identification test is conducted with participation of my coauthor in development of theory and practical algorithms -
Mike Poluektov. He is also a coauthor in multiple publications
About the data
The data is found via Google search. We've found several publicly available datasets and tested one of them so far. The link to the
data site (DAISY) was found in
the article of Torbjorn Wingren.
We very appreciate every effort to provide data recordings for identification of physically existing objects and will
continue this path of testing real data. We will keep publishing identification results as soon as we get them.
Although we appreciate the efforts of researchers in collecting and publishing data, we have to add some critical
remarks about the data we've tested so far. First reason for constructive criticism is that data samples are
too short. Obviously, the data has been recorded by certain automatic registration tools, so we don't see reason why they all
are about 1,000 points and not 10,000. Second constructive criticism remark is that there must be two samples,
one of which is used for identification and another for accuracy test. When people use neural network algorithms,
they can build absolutely accurate model by blowing up the size of the model. But going over the reasonable limit with
the number of parameters can be seen on testing of identified model by an independent realization which have
not been used in identification process.
At the moment we've tested only single input models. The accuracy of the models is about 2 percent, that means
the average difference between modelled and recorded output value is near 2 percent. Certainly, with Urysohn model
we could provide absolutely accurate model (with zero discrepancy), but we put some reasonable limit on the
size of Urysohn operator based on expected view of the kernel. That is, of course, subjective criterion, but
this is the best we could do with this data. As we've said for the proper accuracy test multiple data samples
are needed.
Test results
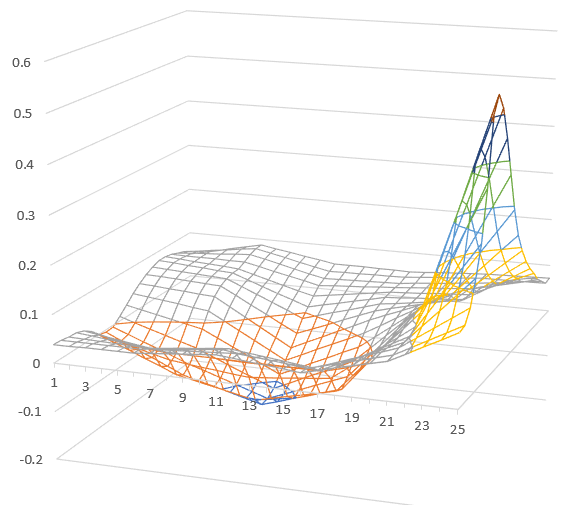
Below is the name of the tested object and the short fragment of overlapped actual and modelled outputs.
| [96-009] Data from a flexible robot arm | 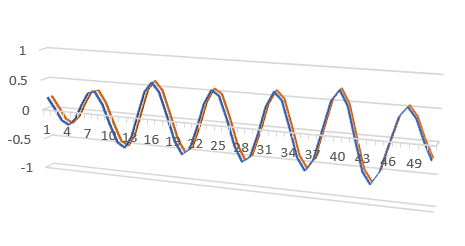 |
| [96-008] Wing flutter data | 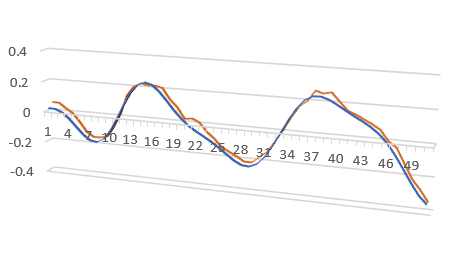 |
| [96-006] Data of a laboratory setup acting like a hair dryer | 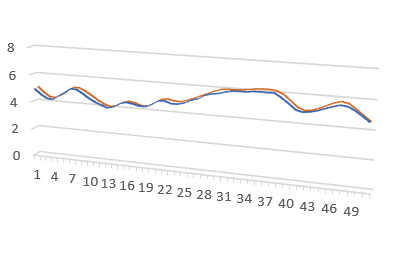 |
| [96-004] Data of the ball-and-beam setup in STADIUS |  |
|