Quantized Urysohn Filter
This is a non-traditional HOME page of large research. Instead of common phrases about nonlinear models, data filtering, artificial intelligence and system identification, we prefer to show a concept, which lays in foundation of new form of artificial intelligence.Observing of deterministic system and having indexed inputs $x[i]$ and outputs $y[i]$ recorded or processed by an automatic system, we can identify the following model by a few computational operations:
$$y(t) = \int_{0}^T U[x(t-s),s]ds. $$
Input $x$ depends on time or observation index $i$ for discrete case. It is an argument of a kernel $U[\cdot, \cdot]$, which needs to be identified by $x$ and $y$ sequences without prior assumptions of how this kernel may look like. We can do that by 10 lines of code.If the signals are registered by digital equipment, they are provided as arrays with common notations $x[i]$, $y[i]$. The kernel is also an array $U[i, j]$ and here is the code fragment that do the trick:
for (int i = T - 1; i < N; ++i) {
double predicted = 0.0;
for (int j = 0; j < T; ++j) {
predicted += U[(int)((x[i-j] - xmin) / deltaX), j];
}
double error = (y[i] - predicted) / T * learning_rate;
for (int j = 0; j < T; ++j) {
U[(int)((x[i-j] - xmin) / deltaX), j] += error;
}
}
Obviously, $N$ is size of input, output arrays, $T$ second size of kernel, $deltaX$ is quantization step for $x$
and $learning-rate$ is computational filter for inaccurate data (must be within (0,1] interval). The identified array $U[\cdot, \cdot]$ may be shown as a grid structure with the values in nodes.
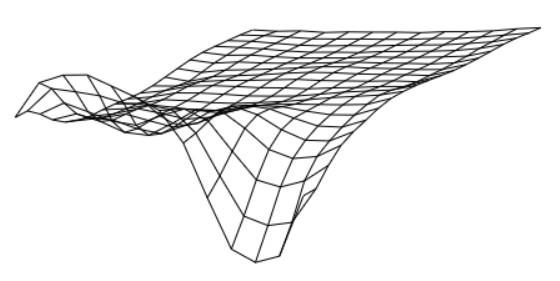
All that may sound like an elegant solution for a particular mathematical problem of identification of nonlinear dynamic system, but, actually, it can be used as elementary brick in a large complicated structure functioning like artificial intelligence. And identified operator is a small part of it similar to a single neuron in a network.
The site developers dedicated this resource to provide an experimental and theoretical proof for the following conceptual statements.
- The quantization of input is not necessary part of the model. All models can be identified as continuous functions.
- The identification algorithm can be upgraded to support models with multiple inputs $$y(t) = \int_{0}^T U[x_1(t-s), x_2(t-s), ..., x_k(t-s), s]ds. $$
- The models may be identified even when applied in cascading sequence
$$y(t) = \int_{0}^T U[x(t-s),s]ds $$
$$z(t) = \int_{0}^T V[y(t-s),s]ds $$
only by first input $x(t)$ and end output $z(t)$, when intermediate signal $y(t)$ is unobserved.
- When arranged in a tree, the models form a structure that functions like artificial intelligence and this structure can be built by input output data by some training process similar to other forms of AI.
The recommended reading sequence is left-hand-side menu, top to bottom.







