Non-Huffman binary tree
In 1952 David Huffman slightly improved method of building binary trees for data compression. The previous method of Fano-Shannon was not actually that bad and difference is laughably small - fraction of a percent or even no difference for some data. Non-the-less, since Huffman tree is formally optimal or best possible, his method pushed away Fano-Shannon tree. New adaptive techniques that start emerging in 1990th make that fraction of percent irrelevant because in adaptive methods the tree is built on the preceding data and applied on the further fragment. In this case the efficiency depends on precision in estimation of probability for every symbol in data that have not yet seen, and the errors are far from the fraction of a percent. In adaptive algorithms the tree is updated or replaced along the data processing, sometimes after processing of every 1000 elements, which introduce new requirement of small number of elementary operations in building the tree. I offer another technique of building binary tree for data compression. Generically this tree is not Huffman, although may coincide in some cases and support basic principle of Huffman tree, where most frequent symbols expressed by shorter codes. Opposite to a Huffman tree this technique allows quick update or replacement of the tree, which makes this algorithm preferable when using in adaptive encoding.Algorithm
There is no need to explain Huffman and Fano-Shannon coding. It looks to me that everybody in the world knows how it look like, or, may be, everybody who reads this article.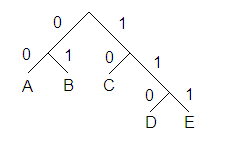
When mostly static data compression methods were used the trees were saved to compressed files in the compact form. In this form only bit length for representation of every symbol needs to be saved, as it is shown in the table below
| Symbol | bit length | code |
| A | 2 | 00 |
| B | 2 | 01 |
| C | 2 | 10 |
| D | 3 | 110 |
| E | 3 | 111 |
The tree can be recreated when bit lengths are known by adding 1 to every next code and shifting after addition to the new length, when necessary. There are some other important properties. When built correctly the last code contains only positive bits. If we assign conventional frequency 1 to all elements in the bottom row and double it when moving to every new bit length and then add all frequencies together we get number expressed as power of 2. Presume imaginary message contains one D and one E also two A, two B and two C, all frequencies together makes 8. That is true for every completed binary tree. That property can be used for quick construction of binary tree. Presume a particular message contains 253 letters A, 190 letters B, 185 letters C, 70 D and 38 E. The suggested in this article technique can be defined by several steps:
1. Sort symbols and add all frequencies.
2. Round up total for all frequencies to the nearest power of 2.
3. Round every frequency down to the nearest power of 2.
4. Moving top to bottom in the sorted list double every frequency if possible to do that without exceeding new rounded up total.
5. Repeat step 4 until sum of all frequencies becomes equal to new rounded up frequency.
6. Difference in bit length between rounded up total and new modified frequency is the bit length for binary tree.
All steps are shown in the next table
| Symbol | frequency | rounded down frequencies | first run | second run | bit length for tree |
| A | 253 | 128 | 256 | 256 | 2 |
| B | 190 | 128 | 256 | 256 | 2 |
| C | 185 | 128 | 256 | 256 | 2 |
| D | 70 | 64 | 128 | 128 | 3 |
| E | 38 | 32 | 64 | 128 | 3 |
| total | 736 | rounded up total = 1024 | current total = 960 | current total = 1024 | - |
So, we sort all symbols in descending order. Total is 736 and it is rounded up to 1024, while every frequency rounded down. Then we double every frequency when we can do that without exceeding 1024 after addition of all new frequencies. We do this operation only once for every element moving top to bottom. On the second run we can see that we can not double top frequency and next one and next one and so on until the very last one. Second run makes the balance and we find bit length difference between total and current, which makes the bit lengths for trees. In this particular example the tree match Huffman tree but it is not true for every data set and, in general case, the tree constructed that way, is different from Huffman tree.
Numerical implementation
Since all operations involve power 2 numbers the building of this tree is extremely fast. The longest operation is sorting frequencies. Even this operation can be avoided in additional optimization mechanism. In suggested algorithm the sorting is implemented during encoding and decoding on every step. When list of symbols is already sorted any new occurrence may need only one switch in sorted list but even this single switch occurred not very often. This adaptive sorting routine is explained in details in another article . In this sorting procedure the symbols are replaced while coding and decoding in the same way that provides additional compression. For example, we replace the tree after every 4096 elements, which makes our total as power of 2 already, but between these updates, let say symbol E became most frequent. In this case symbol E is switched with A in encoding as soon as it became most frequent even before the tree is replaced.The DEMO of working program is shown in the link on the top.
Non-optimality
The noticeable difference with Huffman tree and suggested tree can be seen only for the cases of small alphabets. As it is known in case of small alphabets any binary tree would be the wrong choice and the right choice is arithmetic coding. Binary trees are justified for large alphabets and normally distributed frequencies. In this case the difference in compression due to non-optimality can not be observed, but the improvement in performance can be noticed. The example shows the usage of this tree in context modeling, where large number of independent trees is constructed for every context and applied for data that are not yet occurred. Obviously, the context modeling is critical for compression ratio and not fraction of percent lost while replacing Huffman tree on other binary tree. The trees are not saved into compressed data. The program starts from multiple default trees and update them during encoding process, only bits are going to output, which makes compressed data independent of processor type. This technique is convenient for large alphabets (like 2000 and more).Andrew Polar, July, 2010.