| Adaptive Arithmetic Coder |
| 1. Entropy Deflator | Demo of adaptive entropy deflator, it reduces entropy by replacing most frequent symbols by smaller values |
| 2. RunCoder1 | Demo of adaptive order 1 range coder |
| 3. RunCoder15 | Same as RunCoder1 but with more clear code and much faster because it allows writing output by large chunks |
| Similar programs provided for comparison |
| 4. Context compressor | Context encoder written by Smirnov using Subbotins range coder |
| 5. Quick LZ | Quick LZ data compressor by Lasse Mikkel Reinhold |
| 6. ZIP78 | Elementary 800 lines compression tool, written on technologies known since 1978. |
The concept
Adaptive arithmetic coding is slightly customized switch to a different base. If we consider two numbers 136 and 24 expressed in octal base and want to convert them into decimal base we apply formula:1*82 + 3*81 + 6*80 = 94
2*81 + 4*80 = 20
Same technique applies to longer number 1346132. But if number contains only these symbols 1,2,3,4,6, there is no 0,5 or 7, we can make it shorter. In case some other context properties are available such as number 3 always followed by 2 or 4, it is possible to utilize this property either. For explanation we consider two conditional groups of symbols 1,3,6 and 2,4. We call first group blue and second group red. Now we introduce new detail. We consider distance to the next symbol in sorted list and associate this distance to each symbol. For example, if 1 is followed by 3 in a sorted list 1,3,6 we associate distance 2 with symbol 1 and so on. The last symbol in the list gets distance to the base. We show all distances and symbols involved into our elementary experiment in the tables below
Blue data
|
Red data
|
The classical arithmetic formula for converting of octal number 1346132 into base 10 number is follows
1*86 + 3*85 + 4*84 + 6*83 + 1*82 + 3*81 + 2*80 = 379994
To turn it into sophisticated adaptive arithmetic coder we need to multiply every next term in expression by the distance associated with previous symbol in manner shown below
1*86 + 2*[3*85 + 3*[4*84 + 4*[6*83 + 2*[1*82 + 2*[3*81 + 3*[2*80] ] ] ] ] ] = 636736
This is only change we need comprehend to become guru in adaptive encoders. The result 636736 can be converted back to sequence in pretty much the same way as in a classical numbers theory. To identify first number we divide 636736 by 86 and find interval where this value belong. 636736/86 = 2.42. Since 2.42 is between 1 and 3 we identify fist symbol as 1 and when it is identified we remove it by subtracting 1*86 from both parts and dividing both parts by 2. If we continue in the same way we extract all symbols from number 636736.
The computed value 636736 is not the shortest form of octal number 1346132. In order to make it shorter we need one more operation. The decoding may still go right if we choose number slightly larger 636800, for example. Being more precise we can freely choose the number from the limits LOW and HIGH, where LOW limit is already computed as 636736 and HIGH limit is
HIGH = LOW + 2*3*4*2*2*3*2 = 637312,
where numbers in a product are distances associated with correspondent symbol in the message. As we can see the convenient number is 637000. The selected number should be lower than HIGH but may be equal to LOW. The process of encoding and decoding is shown clearly in the tables below. The division performed for integer operands. We show red data and blue data. In decoding we need to identify number from the correct set either blue or red, so this is the matter of adaptive coding. Since encoder and decoder see the same context they can synchronously switch to different tables. In decoding we know that any symbol after 3 belong to a different set.
Encoding table
| Data type | Symbol * base position | Distances | Total in row |
| Blue | 1*86 | none | 262144 |
| Blue | 3*85 | 2 | 196608 |
| Red | 4*84 | 2*3 | 98304 |
| Blue | 6*83 | 2*3*4 | 73728 |
| Blue | 1*82 | 2*3*4*2 | 3072 |
| Blue | 3*81 | 2*3*4*2*2 | 2304 |
| Red | 2*80 | 2*3*4*2*2*3 | 576 |
| none | none | none | LOW = 636736 |
Decoding table
| Remained number | Identification | Symbol | New remained number |
| 637000 | 637000/86 = 2 | 1 | [637000-1*86]/2 = 187428 |
| 187428 | 187428/85 = 5 | 3 | [187428-3*85]/3 = 29708 |
| 29708 | 29708/84 = 7 | 4 | [29708-4*84]/4 = 3331 |
| 3331 | 3331/83 = 6 | 6 | [3331-6*83]/2 = 129 |
| 129 | 129/82 = 2 | 1 | [129-1*82]/2 = 32 |
| 32 | 32/81 = 4 | 3 | [32-3*81]/3 = 2 |
| 2 | 2/80 = 2 | 2 | finish |
Those who have programming experience can see that multiplication and division by 8 is only binary shift. The problem with long products is solved by approximate calculations. As you can see in every encoding step the resulted product is multiplied by new number so it is implemented as mantissa (usually 16 bit integer) and exponent. After every new multiplication we update mantissa and keep track on exponent that provides additional shift. In real compression algorithm the distances 2,3,4,2,2,3,2 that we called distances to the next number in sorted list are frequencies of occurrences. The base always may be chosen as power of 2. In case message contain all possible symbols of octal number 0,1,2,3,4,5,6,7 our generalized method turn into classical because all distances are equal to 1.
Outstanding scientific issues
The provided above example seams very simple but there are two scientific issues that left. First is a proof that shown technique really compress data to a theoretical limit defined by entropy and second is about convergence, that means theoretical proof that decoding will always work for, at least, precise data. First proof is provided by myself in anonymous Wikipedia article and second one will be considered below. Presume our alphabet contains 3 symbols following in order (S3, S1, S2, …), for which we can define values called frequencies and cumulative frequencies, which magnitudes may be shown graphically in the picture below
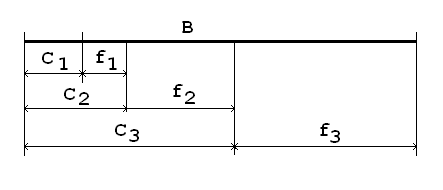
C1 can be any non-negative number,
C2 = C1 + f1,
C3 = C2 + f2,
B = C3 + f3,
where B is the base. If we limit our sequence to 3 symbols only, the LOW and HIGH limits are calculated as follows
LOW = B2 *C3 +B*f3*C1 + f3*f1*C2
HIGH = LOW + f3*f1*f2 =B2 *C3 +B*f3*C1 + f3*f1*(C2 + f2)
Since our selected result must be in range [LOW, HIGH) we may introduce variable g, that takes values from interval [0, f2), and present result as
RESULT = B2 *C3 +B*f3*C1 + f3*f1*(C2 + g)
We need to poof that for any g from [0, f2) first step in decoding surely identifies first symbol as S3 based on C3. Well, that is elementary, if we divide RESULT by B2 the computed value will be between C3 and C3 + F3 because fraction
[B*C1 + f1*(C2+g) ] / B2 is less than 1.
Why it is less than 1? Because C1 + f1*(C2+g) / B is less than B and, that, in turn, because (C2+g) / B is less than 1 for any g from defined interval. When C3 is identified it can be excluded from result in the way already shown. Recursively, this example can be applied for the message of any size. That also makes obvious that RESULT for message of size n is less than Bn.
History
Some engineers and researchers call this technique of arithmetic encoding as range encoding because it computes result by narrowing down the range starting from [0, nn). The only difference with classical arithmetic encoding is that the latter computes result as narrowing range starting from interval [0,1). Switching between these two methods can be done by simple division of all numbers involved in computation by nn. The new name for the method was assigned because many people wanted to present it as formally different and on that reason patent free. All sources and tutorials for range encoding provide link to the same article , that appeared in Internet near 2000 and is not readers friendly. The encoding technique shown in the article is very close to numerical example shown above. The decoding technique, however, is so unclear that is subject to interpretation. There is no proof that suggested compression compresses data to entropy limit and, although it states that this technique can be applied as adaptive, this mentioned adaptive technique is not shown in a way that it could be reproduced. The article does not reduce the raw idea, poorly presented in it, to a practice and on that reason could not be considered as prior art. We may consider as prior art the big number of successful implementations of range coders written and published near year 2000 where this article was mentioned to back up the concept.
On the reason that integer concept was unclear, it slipped out the mind of many researchers and engineers, who were filing patents between 1980 and 2000. In all patents filed during that period arithmetic encoding is defined as computation of proper fraction, which may open debates of novelty. Since so many people may be benefited from this hidden out of the view but public material I decided to conduct my personal investigation of its authenticity. The red flag was not only the negligence in explanation but the fact that Glen Langdon researcher for IBM cited this article in An Introduction to Arithmetic Coding, IBM J. RES. DEVELOP. VOL. 28, No 2, March 1984 without ever mentioning integer concept and kept filing patents explaining the concept of arithmetic coding as computing of growing on every step proper fraction. No matter how it all may look like the article appeared to be authentic and G. Nigel N. Martin is a real person who confirmed for me personally that he conducted this research back in 1979. It is interesting that in the above link with the list of his publications this work is not mentioned, although it is the one for which the name G.N.N. Martin is most frequently mentioned in Internet.
Large alphabets
The size of the alphabet can create a specific problem. In adaptive procedure the probabilities of occurrence for every symbol must be recalculated periodically. When size of the alphabet approach 10,000 the execution slows down. The answer to large alphabets is symbol replacement technique. In this method symbols are simply replaced by sequential indexes 0,1,2,... according to their frequencies of occurrence, where most frequent numbers have least indexes. The processing then performed bitwise where each bit from each symbol is sent to a different binary coder but the output streamed to one expression. For example, let say we have alphabet A,B,C,D and a message of 1000 symbols where symbols occur according to the following table| Symbol | Frequency | Binary expression |
| A | 600 | 00 |
| B | 300 | 01 |
| C | 80 | 10 |
| D | 20 | 11 |
If we process first bit of every symbol by one binary coder we get 0.47 bits/symbol. If we do the same thing with second bit of every symbol we have 0.90 bits/symbol. So, we have 1.37 bits/symbol overall. If we calculate entropy by the classical formula we have about the same number 1.367 bits/symbol. It is possible to prove theoretically that when data are distributed normally the compressed data size is in accordance with Shannon entropy and when alphabets are large the data are almost always have normal distribution.
Entropy reduction
Replacement of symbols mentioned above can be made byte by byte, when we replace most frequent bytes by lower integers. In this case the entropy of data is changed but the size of data is the same, which is very convenient. In case this procedure is adaptive no any additional data have to be saved. To make this procedure adaptive symbol should be predicted before it is replaced and before the statistics is updated.Adaptive sorting routine used in bytewise entropy reducer
While bitwise prediction is clear and do not need any specific explanation other than working coding example, bytewise prediction is much more complicated. In bytewise prediction we predict next byte according to set of previous bits, so we have to collect statistics for every possible combination for selected context size. For example, if our selected context size is preceding 12 bits. All combinations cover binary fragments from 000000000000 to 111111111111. All 4096 combinations have to have statistic array of 256 symbols, where each element contains the number of occurrence of particular byte. Besides that we need resort these symbols frequently and use it for replacement of every byte by its position in the sorted list. In addition to what is said already we want to resort array after every new symbol in order to accumulate every new information. Although it sounds very complicated it is actually not and all that is implemented in very short (about 80 lines) quick routine that handles 1 Meg. over 0.3 sec. For this purpose I introduced special quick sort algorithm that may not be completely new and is based on the fact that in already sorted array any new symbol may require only two elements switch.In sequential symbol processing the desired action is to update sorted data on every step. The experiments with some quick sorting algorithms such as QSORT, HSORT show that although they are extremely fast their usage in periodic sorting of data slows down the execution significantly. From the other side after every single frequency increment we may need to switch only two elements in array of collected frequencies if array was sorted before it. For example, having sorted frequencies in array as follows 107, 100, 99 , 99, 99 , 23 we need to switch third element with fifth element in case fifth element is incremented (we counting positions from 1). In case first, second or sixth element is incremented no action is required. In addition to sorted array of frequencies we need keep track of original position of every element because we have to replace this original value reversibly. For successful decoding we need also maintain addresses for quick reversing of replaced value. After some experimenting I ended up with rather simple routine that uses three arrays. It works fast but I presume there is still room for further optimization. Since algorithm is elementary there are high chances that it was used before. I did not conduct the search and presume it is not patented because of obviousness.
Let us consider these three array in a table below
| Encoder returned symbols | S[i] | 2 | 1 | 3 | 0 |
| Frequencies | F[i] | 150 | 190 | 150 | 210 |
| Decoder returned symbols (inverse) | I[i] | 3 | 1 | 0 | 2 |
| Position index | i | 0 | 1 | 2 | 3 |
The elements of the frequency array are not switched in position but incremented on every occurrence (++f[i]). The top row elements are codes returned in encoding. For synchronization we get encoded value and output encoded value before updating the table. The index array at the bottom shows the position of elements for explanation. It is not physical memory allocation. The encoding is simple array look up. We replace 0 by 2, 1 by 1, 2 by 3 and 3 by 0 in encoding step. In decoding we replace data according to inverse array, we replace 0 by 3, 1 by 1, 2 by 0 and 3 by 2. In our look up structure if S[i] = k then I[k] = i. We can see also that we need change encoding/decoding arrays only in case value 2 occurs for our particular data. In other cases we only increment correspondent frequency. If value 2 occurs (i=2) we increment F[2] and have F = {150, 190, 151, 210}. Now we rearrange S[i] and I[i] to match new data distribution. Obviously we need to switch two elements in both arrays. The function UpdateTables quickly locate these two elements and switch them. The table after update looks as follows:
| Encoder returned symbols | S[i] | 3 | 1 | 2 | 0 |
| Frequencies | F[i] | 150 | 190 | 151 | 210 |
| Decoder returned symbols (inverse) | I[i] | 3 | 1 | 2 | 0 |
| Position index | i | 0 | 1 | 2 | 3 |
The first and third row in last table look identical but that is a coincidence that exists for small tables. In processing of real data the predicted values are 4 to 8 bit long and array sizes are between 16 and 256 accordingly.
There is similarity between this method and Move-To-Front method. The difference is that in MTF every symbol is replaced by its position according to last occurrence while in suggested method the position depends on frequency. The programming implementation includes also forgetting mechanism, where frequencies collected long ago are forgotten and latest occurrence have higher influence. On that reason suggested method is considered as generalization of MTF.
Experimental results
The file set for testing is taken from Maximum Compression. The compression ratio is shown relative to original data.| Encoder\File | A10.jpg | acrord32.exe | english.dic | FlashMX.pdf | fp.log | mso97.dll | ohs.doc | rafale.bmp | vcfiu.hlp | world95.txt |
| RunCoder1 compression ratio | 0.999 | 0.574 | 0.366 | 0.909 | 0.281 | 0.653 | 0.401 | 0.304 | 0.395 | 0.465 |
| RunCoder1 compression time | 0.421 | 1.046 | 0.828 | 1.765 | 3.890 | 1.109 | 1.015 | 0.796 | 0.890 | 0.640 |
| Runcoder1 decompression time | 0.453 | 1.140 | 0.890 | 1.859 | 4.405 | 1.187 | 1.109 | 0.874 | 0.954 | 0.718 |
| Subbotin compression ratio | 1.018 | 0.618 | 0.377 | 0.916 | 0.333 | 0.691 | 0.444 | 0.384 | 0.467 | 0.454 |
| Subbotin compression time | 0.249 | 0.937 | 0.859 | 1.249 | 3.921 | 0.968 | 1.046 | 1.015 | 0.890 | 0.640 |
| Subbotin decompression time | 0.296 | 1.109 | 1.015 | 1.453 | 4.687 | 1.156 | 1.296 | 1.265 | 1.062 | 0.750 |
| QuickLZ compression ratio | 1.000 | 0.521 | 0.355 | 1.000 | 0.086 | 0.657 | 0.257 | 0.421 | 0.249 | 0.352 |
| QuickLZ compression time | 0.046 | 0.218 | 0.187 | 0.312 | 0.562 | 0.249 | 0.156 | 0.203 | 0.156 | 0.140 |
| QuickLZ decompression time | 0.031 | 0.093 | 0.062 | 0.062 | 0.250 | 0.093 | 0.078 | 0.062 | 0.062 | 0.062 |
| EntropyDeflator compression ratio | 0.997 | 0.556 | 0.252 | 0.924 | 0.088 | 0.646 | 0.361 | 0.333 | 0.309 | 0.382 |
| EntropyDeflator compression time | 0.375 | 0.453 | 0.187 | 1.328 | 0.703 | 0.547 | 0.453 | 0.188 | 0.281 | 0.234 |
| EntropyDeflator decompression time | 0.328 | 0.360 | 0.156 | 1.031 | 0.656 | 0.422 | 0.390 | 0.140 | 0.234 | 0.188 |
| ZIP78 compression ratio | 1.004 | 0.465 | 0.306 | 0.862 | 0.072 | 0.586 | 0.242 | 0.306 | 0.221 | 0.301 |
| ZIP78 compression time | 0.343 | 0.453 | 0.765 | 1.327 | 0.344 | 0.515 | 0.343 | 0.453 | 0.218 | 0.171 |
| ZIP78 decompression time | 0.281 | 0.265 | 0.109 | 1.000 | 0.172 | 0.344 | 0.250 | 0.110 | 0.112 | 0.094 |
Conclusion
RunCoder1 is streaming adaptive entropy coder that processes bytes one-by-one while reading. The code is about 600 lines and it is supposed to be used as part of archiver not as whole and only part of it. The expected resusult is achieving compression near other context encoder, written by M.Smirnov. RunCoder15 is improved version of RunCoder1. The speed is significantly faster because data is read and written by large chunks not byte by byte. The published version process data in memory. RunCoder15 outputs data in format independently if big endian processor or little endian processor was used.Andrew Polar, Feb. 2009.
Last modification, July. 2010.