Kolmogorov's formula
Demo code download3b1b video
Kolmogorov superposition theorem states that continuous function of several variables can be adequately replaced by superposition of multiple functions of one variable:
$$ f(x_1, x_2, x_3, ... , x_n) = \sum_{q=0}^{2n} \Phi_q\left(\sum_{p=1}^{n} \phi_{q,p}(x_{p})\right) $$
Obviously, it is $2n + 1$ parallel discrete Urysohns with output static nonlinearity followed by each of them. In the article about modelling of two sequential Urysohns we showed that for the approximation of deterministic object only one Urysohn plus nonlinearity is enough. The accurate quantity for exact representation is $2n + 1$, where $n$ is number of discrete input impulses.
It is excellent to know that such representation exists, unfortunately Kolmogorov did not provide instructions how to find it. In this article we share an experience of finding this representation.
Assuming that we have initial approximation in piecewise linear form, we can tune initial model into more accurate one by the same technique that is used for identification of a single Urysohn object. $\Phi$ is a set of multiple static nonlinearities and is a Urysohn model itself. That means $\Phi$ can be adjusted for known arguments
$$arg_q = \sum_{p=1}^{n}\phi_{q,p}(x_{p}),$$
and arguments can be adjusted for known increments $\Delta arg_q$
$$ f(x_1, x_2, x_3, ... , x_n) = \sum_{q=0}^{2n} \Phi_q\left(arg_q + \Delta arg_q\right). $$
For each known left-hand side $f$ of above formula the set of small argument increments, that improves model, can be determined and the other set of Urysohns can be adjusted as well.
This algorithm is implemented in downloadable coding demo. The test data is generated by two sequential Urysohns of rather complex shape shown below
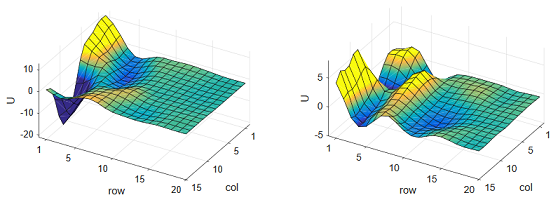
When program is executed, the new data is generated for each run and end result slightly varies. The residual discrepancy for unseen data is usually 2 to 3 percent and for training data between 1 and 2 percent. In case when single Urysohn is applied for generated data, the residual discrepancy is between 10 and 15 percent.



