Mathematically arithmetic encoder is reversible technique of conversion of sequences of proper fractions to a single proper fraction. If we bring all fractions to common denominator arithmetic encoder turns into range encoder. In the paper we consider technical details of both arithmetic and range encoder and some patent issues. The topic marked as [prerequisite] is necessary for understanding of further material. It may be familiar to many readers with experience in data compression and simply skipped.
Those familiar with the subject and need the code only can skip the paper
| rangemapper.cpp | Latest and most advanced. Round trip with encoding/decoding self-test. | RunCoder0.cpp | Round trip with encoding/decoding self-test. |
| RanCode.cpp | Complete self-test round trip with encoding/decoding |
| RanCodeAdp.cpp | Complete self-test round trip for adaptive range coder |
| RanCodeBigEnd.cpp | Complete self-test round trip for code running in both big and little endian processors |
Benchmark
While the compression ratio for many arithmetic encoders varies within very small range such as 1 percent, the time of code execution may be different by the factor of 10. Since the performance is very important issue I suggest simple benchmark project that compares considered in this paper encoder called RANCODE to FastAC and other encoders. Some other benchmarks can be found in benchmark report , where several other encoders are compared to FastAC. Those who want to rerun my tests can download simple Windows consol project that makes round trip for tested encoders and prints result in the following way.
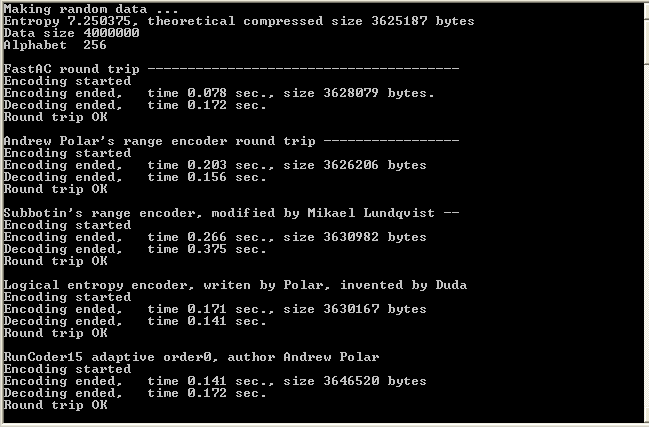
The project is done in Visual Studio 2005, but the code is simple to be compiled in other OS as well with possible cosmetic changes.
[prerequisite] Data modeling and entropy coding
Data modeling is reduction of the data size based on position of symbols due to repetition, periodic similarities or other type of predictability. The following abbreviations are keys to search for different algorithms of data modeling
| RLE | Run-length encoding |
| LZ77 | Lempel-Ziv |
| LZW | Lempel-Ziv-Welch |
| BWT | Burrows-Wheeler transform |
| FFT | Fast Fourier transform |
| WT | Wavelet transform |
| KLT | Karhunen-Loeve transform |
When all advantages of positioning are exhausted the last reserve is statistical coding. It applies when some symbols occur more frequently than the others. Sometimes it is called entropy encoding and uses statistical distribution of the symbols ignoring the positions. For entropy encoding message AAABBBBBCCCCCCC is not better than CABBCCACBABCCBC because data distribution is the same. This message can be compressed to a certain limit independently on the order of the symbols.
[prerequisite] Arabic numbers and the bit length of a number
Arabic numbers is not only set of symbols 0123456789 but also polynomial presentation of the number. For example, number 457 is
4 * 10 2 + 5 * 10 1 + 7 * 100
Same polynomial presentation of a number may be applied for any ordered set of symbols starting from size 2. The number of different symbols used for notations is called base. For example the word MATH may be interpreted as a number with the base 26 if we presume A=0, B=1 and so on until Z=25
| 12 * 263 + | 0 * 262 + | 19 * 261 + | 7 * 260 | = 211413 |
| M | A | T | H |
We can see that same numbers have different lengths in different base presentations. The number of symbols required for presentation of a number in a different base may be approximately estimated by logarithm logbase. For example,
log26(211413) = 3.76
So we can see that number 211413 may be expressed in about 4 symbols in base 26 integers. Since all digital information is stored as base 2 integers we may want to recalculate lengths of numbers from decimal to base 2 integers. This is how log2 came to a picture. It is switch from one alphabet to another. From this place on we will use base 2 logarithm only and base notation will be omitted.
[prerequisite] Entropy as compression limit
We consider compression limit for statistical compression only. It is logical to expect that compression is sufficiently good if the length of compressed message is not longer than the number of distinct messages with given statistical data distribution. The reason for such limit must be clear. We can sort all messages, enumerate them and transmit the sequential position index instead of message. Looks like ideal solution, but this sequential index also have size, which is limited by possible variety of messages. This variety obviously is number of permutations or number of possible ordered sets taken from collection without return. For example if our collection is 0,0,1,1,2 and we make all possible lists without return it looks like follows
|
0 0 1 1 2 0 0 1 2 1 0 0 2 1 1 0 1 0 1 2 0 1 0 2 1 0 1 1 0 2 |
0 1 1 2 0 0 1 2 0 1 0 1 2 1 0 0 2 0 1 1 0 2 1 0 1 0 2 1 1 0 |
1 0 0 1 2 1 0 0 2 1 1 0 1 0 2 1 0 1 2 0 1 0 2 0 1 1 0 2 1 0 |
1 1 0 0 2 1 1 0 2 0 1 1 2 0 0 1 2 0 0 1 1 2 0 1 0 1 2 1 0 0 |
2 0 0 1 1 2 0 1 0 1 2 0 1 1 0 2 1 0 0 1 2 1 0 1 0 2 1 1 0 0 |
Without return means if symbol is taken it is no longer in collection. The formula is
5! / (2! * 2! * 1!) = 30
It can be quickly derived. Every particular message from the table has same probability of occurrence equal to the product of probabilities of occurrence for every symbol. Same as pulling balls with numbers from the box in the blind. For example for 00112 it is
2/5 * 1/4 * 2/3 * 1/2 * 1/1
2/5 is probability to pick first zero, 1/4 is probability to pick second zero and so on. The inverse of this probability is number of combinations. Obviously it does not depend on the order in which balls are pulled from the box. The industry, however, approved another limit that is similar but needs an explanation. According to Claude Shannon [1] ideal encoder must express every symbol by -log(p) bits. We can easy obtain this limit by replacing factorials in above expression by powers
55 / ( 22 * 2 2 * 11) = 195
It can be calculated as inverse of the product of probabilities when we presume that they are not changing along the message i.e. always 2/5, 2/5 and 1/5. The difference looks significant only for short messages, but when the length is over 1000 symbols it is only fraction of percent and for 1000000 symbols practically disappear. The numbers itself may have noticeable difference but we consider bit lengths that are very close. It can be explained by Sterling formula used for approximation of factorial for large numbers, according to which
log(n!) is approximately log(nn) - n
To back up this statement we can compare results for dual alphabet with same proportion and different length of the message
| n | f1 | f2 |
log { ( n n ) / ( f1 f1 * f2 f2 * ... * fk fk) }
Estimated number of bits in a message |
log { ( n!) / ( f1! * f2! * ... * fk!) }
Exact number of bits |
| 10 | 1 | 9 | 4.7 | 4 |
| 1000 | 100 | 900 | 469 | 465 |
| 10000 | 1000 | 9000 | 4689 | 4684 |
The last part in this topic is to show how it all related to entropy. In order to estimate number of bits we apply logarithm to the number of possible permutations and replace factorials by Sterling approximation
5*log(5) - 2*log(2) - 2*log(2) - 1*log(1) + 5 - 2 -2 -1
If we divide this number by the number of symbols we have limit expressed in bits per symbol
log(5) - 2/5*log(2) - 2/5*log(2) - 1/5*log(1)
We can express log(5) as 2/5 * log(5) + 2/5 * log(5) + 1/5 * log(5) and change previous expression into following
- 2/5*log(2) + 2/5*log(5) - 2/5*log(2) + 2/5*log(5) - 1/5*log(1) + 1/5*log(5) =
- 2/5*log(2/5) - 2/5*log(2/5) - 1/5*log(1/5) =
- p1log(p1) - p2log(p2) - p3log(p3)
which is the entropy. We can see that for the entropy encoder the bit length of encoded message must be not longer than
n log(n) - f1log(f1) - f2log(f2) - ... - fmlog(fm)
where n is size of the message, fi are frequencies and m is size of the alphabet. It is slightly converted entropy formula but more clear and easier for use. For the large messages this number is very close to bit length of number of possible permutations, so reaching this limit is sufficiently good for entropy or statistical encoder.
Arithmetic encoding
Static arithmetic encoder starts from collection of statistics. We do it for previous example changing 20011 to CAABB
| Symbol | Cumulative probability Ck | Probablity Pk |
| A | 0.0 | 0.4 |
| B | 0.4 | 0.4 |
| C | 0.8 | 0.2 |
Cumulative probability is sum of all previous probabilities in the right column. It starts from 0.0 because there is no previous probability value. While probabilities may be repeated the cumulative probabilities are disjoints and can be uniquely associated with symbols. Next step is computation of two limits LOW and HIGH by formula.
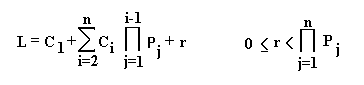 | (1) |
| C1 | ||||
| C2 | P1 | |||
| C3 | P1 | P2 | ||
| -//- | -//- | -//- | -//- | -//- |
| Cn | P1 | P2 | -//- | Pn-1 |
The first column contains cumulative probabilities following top to bottom in the same order as they follow in the message. They are multiplied by probabilities for all previous symbols in a message. The index starts from 1. To obtain result we have to compute products of cofactors in every row and then find the sum of them. I call this visual tool ARCOD pyramid.
There is also one variable value in the formula that can be freely chosen within defined limit. This variable establishes high limit. The meaning of this high limit will be clear later, after calculation of ARCOD pyramid.
| 0.8 | ... | ... | ... | ... | 0.80000 |
| 0.0 | 0.2 | ... | ... | ... | 0.00000 |
| 0.0 | 0.2 | 0.4 | ... | ... | 0.00000 |
| 0.4 | 0.2 | 0.4 | 0.4 | ... | 0.01280 |
| 0.4 | 0.2 | 0.4 | 0.4 | 0.4 | 0.00512 |
| ... | ... | ... | ... | ... | 0.81792 |
The result 0.81792 is not shorter than original sequence. We can reduce the result by special selection of variable r within admitted range. The high limit of the range is product of all probabilities of the message 0.2 * 0.4 * 0.4 * 0.4 * 0.4 = 0.00512. The shortest decimal fraction from semi-open interval [0.81792, 0.82304) is 0.82, which is our final encoded message.
The key to understanding arithmetic encoding is the fact that reduction occurs due to possibility of freely choosing the fraction within certain interval. The computed LOW limit by itself is generally not shorter than original message.
The decoding is performed by matching symbols one by one to probability table and eliminating them. I call matching method BLACK JACK. We have to find maximum possible cumulative probability that can be subtracted from encoded message with non-negative result. For the first step it is 0.8 and recognized symbol is C. When symbol is recognized the result is converted to new shorter message by subtracting cumulative probability and division by probability
(L-C1)/P1
This action is close to elimination first row and second column from ARCOD pyramid. Second step is same elimination of the second row and third column and so on to the end.
In order to back up theoretical part we show one more formula which clearly proves the possibility of recognition
C1 + P1 (C2 + P2 (C3 + P3 (C4 + P4 (C5 + R))))
The formula is another form of ARCOD. When R is chosen correctly C5 + R is recognized because it belongs to certain interval. Since C5 + R less than 1.0 expression C4 + P4(C5 + R) belong to certain interval as well and is recognized also and so on until C1. When C1 is recognized and excluded the remained part is encoded message that starts from C2.
The programming challenge for writing arithmetic encoder is obvious from ARCOD. It is long products of probabilities. The solution was to do computations approximately and express them as mantissa and exponent [2]. In this case we need to add numbers with same size mantissa and different exponents. There is carry-over problem and correct positioning of mantissas relative to each other that is called renormalization. Renormalization occupies chapters in some books for explanation and code for arithmetic encoder is dramatically different from simple algebraic formula. There is way to write encoder without renormalization and fractions and at the same time design around big number of patents. It is called range encoder.
Range encoding
Arithmetic encoder is turned into range encoder by bringing all fractions to common denominator. All fractions in ARCOD have same denominator n, which is size of the message. The products on every line have multiple n denominators. The convenient common denominator is nn. By multiplication of every line in ARCOD pyramid by nn we switch to new pyramid that is range encoder. I call it RANCOD.
| nn-1C1 | ||||
| nn-2C2 | F1 | |||
| nn-3C3 | F1 | F2 | ||
| -//- | -//- | -//- | -//- | -//- |
| n0Cn | F1 | F2 | -//- | Fn-1 |
where Fi are frequencies of occurrence, Ci are cumulative frequencies. Arbitrary parameter also exists. It does not reduce fraction, but can make a long list of zero bits at the tail of the number that can be dropped or saved in shorter form. The algebraic formula is the following
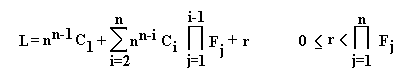 | (2) |
Same as result of arithmetic encoder never exceed 1.0 the result of range encoder never exceed nn. In order to back up the statement that RANCOD is range encoder we reproduce here the example from article written by founding father of range coder [3].
http://www.sachingarg.com/compression/entropy_coding/range_coder.pdf
The example, cosidered in the article, is message fragment NMLNNNKKNML for the probabilities 0.1, 0.21, 0.27, 0.42 correspondently assigned to symbols K,L,M,N. The frequencies and cumulative frequencies are shown in the table below
| Symbol | Frequency | Cumulative frequency |
| K | 10 | 0 |
| L | 21 | 10 |
| M | 27 | 31 |
| N | 42 | 58 |
The RANCOD looks as follows
| # | symbol | nkC | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | Product |
| 0 | N | 10010 58 | 5800000000000000000000 | ||||||||||
| 1 | M | 1009 31 | 42 | 1302000000000000000000 | |||||||||
| 2 | L | 1008 10 | 42 | 27 | 113400000000000000000 | ||||||||
| 3 | N | 1007 58 | 42 | 27 | 21 | 138121200000000000000 | |||||||
| 4 | N | 1006 58 | 42 | 27 | 21 | 42 | 58010904000000000000 | ||||||
| 5 | N | 1005 58 | 42 | 27 | 21 | 42 | 42 | 24364579680000000000 | |||||
| 6 | K | 1004 0 | 42 | 27 | 21 | 42 | 42 | 42 | 0 | ||||
| 7 | K | 1003 0 | 42 | 27 | 21 | 42 | 42 | 42 | 10 | 0 | |||
| 8 | N | 1002 58 | 42 | 27 | 21 | 42 | 42 | 42 | 10 | 10 | 102331234656000000 | ||
| 9 | M | 1001 31 | 42 | 27 | 21 | 42 | 42 | 42 | 10 | 10 | 42 | 22971597848640000 | |
| 10 | L | 1000 10 | 42 | 27 | 21 | 42 | 42 | 42 | 10 | 10 | 42 | 27 | 2000752070688000 |
| 7436023987264575328000 |
As we already explained, in order to complete encoding we have to calculate limit for arbitrary variable r, that is 42*27*21*42*42*42*10*10*42*27*21 = 4201579348444800 and choose result from semi-open interval
[7436023987264575328000, 7436023987264575328000 + 4201579348444800)
The result is 7436028 * 10 15. The result in the article is 7436026. It qualifies as well (not mistake). The limit 4201579348444800 is product of all frequencies for the message. Some results in right-hand side column are slightly different from values in the article. The reason for that is approximation in calculation of product of frequencies in original article. In this example base is 100, but the message length is 11. It is not a mistake. We can presume that message length is 100 and we consider only a fragment. It also illustrates that we can manipulate by probabilities and frequencies within the certain limit.
By the same principle as arithmetic encoder the range encoder reduce message due to possibility of free choice of result within calculated limits. The computed LOW limit by itself is not shorter than original data.
Compression limit
The binary length of encoded result is not longer than log (n n), because it is limited by this number. The trail of zero bits is defined by the length of the product of all frequencies that constitute upper limit for the range in formula (2). That means that bit length of encoded message is
n log(n) - f1log(f1) - f2log(f2) - ... - fmlog(fm)
which is in accordance with Shannon entropy. In our example it must be
11 log (100) - 2 log (10) - 2 log (21) - 2 log (27) - 5 log (42) = 22.18,
which is what we get.
As we can see in expressions of type X log (X) in the last formula the argument of logarithm function is chosen freely. It raises question about optimal choice. If it is possible to alter frequencies or cumulative frequencies in order to obtain better compression. This question was already addressed [8] and the best compression is expected when all frequencies that plugged to the last formula are not altered. Mathematically it is typical problem of constrained extremum. If we limit size to 2 for simple example we can see that we need to find maximum of the functional
n1 log (x1) + n2 log (x2) with constraint x1 + x2 = n1 + n2
where n1, n2 given numbers and x1, x2 are unknown variables. The classical approach to such type of problem is Lagrange multipliers. According to the method the constraint equation with indefinite multiplier L is added to the functional
n1 log (x1) + n2 log (x2) + L (x1 + x2 - n1 - n2)
after which the unconstrained extremum is sought by assigning partial derivatives with respect to x1 and x2 to zero
n1 / (x1 ln(2)) + L = 0
n2 / (x2 ln(2)) + L = 0
Last two equations are consistent if
n1 / x1 = n2 / x2
which along with constraint x1 + x2 = n1 + n2 leads to unique solution x1 = n1 and x2 = n2. The found extremum, strictly speaking, may be either maximum or minimum. It can be found according to the sign of the second order derivative that it is maximum. The functional is not very sensitive to small variation of frequencies and change of frequencies within few percent does not affect compression ratio, so the approximations and rescaling of frequencies does not noticeably change the compression.
Entropy revisited
As we can see the matter of range encoding is computing the limits (LOW and HIGH) on interval from 0 to nn. The range between computed limits (HIGH-LOW) is equal to product of all frequencies where every frequency is repeated as many times as the symbol in the message f1f1 * f2f2 * f3f3 ... fmfm and does not depend on LOW value. Since maximum possible limit for the range is known as nn we may want to find how many intervals are theoretically possible to allocate on this interval. This number
I = n n / (f1f1 * f2f2 * f3f3 ... fmfm)
looks very familiar. As it was already shown the bit length of this number divided by number of symbols is the entropy. We have to assign partial credit on range encoding to Claude Shannon, because entropy carries in implicit form the starting limit for the range encoder nn and width between LOW and HIGH and missing only value for LOW.
It was also shown in the beginning of the article that the actual number of different messages or the number of permutations is significantly lower this theoretical limit I and actually equal to n! / (f1! * f2! * ... * fm!), therefore sub-intervals for every different message are spread apart from each other. We can show this numerically for the first example. It was set of symbols 0,0,1,1,2. The table below shows all 30 permutations and LOW limit computed for every permutation and shown after dash.
| 00112 - 344 00121 - 376 00211 - 456 01012 - 644 01021 - 676 01102 - 764 |
01120 - 860 01201 - 916 01210 - 940 02011 - 1056 02101 - 1116 02110 - 1140 |
10012 - 1394 10021 - 1426 10102 - 1514 10120 - 1610 10201 - 1666 10210 - 1690 |
11002 - 1814 11020 - 1910 11200 - 2150 12001 - 2266 12010 - 2290 12100 - 2350 |
20011 - 2556 20101 - 2616 20110 - 2640 21001 - 2766 21010 - 2790 21100 - 2850 |
The upper limit is 55=3125 and range is 2 * 2 * 2 *2 * 1 = 16. We can see that intervals are indeed spread apart and random number picked from interval between 0 and nn not necessarily represent an encoded message with particular statistical data. For classical arithmetic encoder we may presume same properties for interval 0 to 1.0.
Range coder as generic presentation of the integer in a new base
In case all frequencies in formula (2) equal to 1 the formula turns into classical presentation of integer in a new base. In classical base 10 presentation all symbols 0123456789 are integers that start from 0 and incremented by 1 and the last digit 9 is less by 1 than the base. We may consider this difference as distance to the next digit or distance to the base from the last digit. The set of the symbols constitute the alphabet. In Martins example symbols are 0, 10, 31, 58 and the base is 100. First digit 0 has distance 10 to the next digit, second digit 10 has distance 21 to the next digit and so on. The last one has distance to the base equal to 42. If we present our symbols in base 100 in a classical way the number is
58 * 10010 + 31 * 1009 + 10*1008 + ... = 5831105858580000583110
Reverting this number back to original sequence is trivial. Range encoding introduces multiplication of every addend by the distances to the next symbol in alphabet for all previous symbols (they marked red in the following expression)
58 * 10010 + 31 *1009 * 42 + 10*1008 * 42*27 + ...= 7436023987264575328000
The number is getting larger but can be reduced using arbitrary variable from the certain interval that is defined by the product of all distances. That makes result more compact. When we choose number 7436028000000000000000 for result we do not change result significantly, we simply present number as mantissa 7436028 and exponent 1000000000000000, which allow save or transmit number in more compact form.
The reverting number back to original sequence is conducted in the same way for classical base presentation and for generic one. If we return back to example with presentation of the word MATH as base 26 integer the steps are
211413/263 = 12.028, so the first symbol is M
(211413-12*263)/262 = 0.741, so the second symbol is A
(211413-12*263-0*262)/261 = 19.26, so the third symbol is T
(211413-12*263-0*262-19*26) = 7, so the last symbol is H
We discarded fractional part because it is less than a distance to the next symbol in alphabet. We may also consider that we divided result by correspondent distance Fi on every step, but it is numerically equal to 1 and makes no difference. When number 211413 was computed it was also chosen from the range 211413 + r, where r must be less than 1 and non-negative. Same logic applies to generalized base number. We divide 7436028*1015 by 10010. The result is 74.36. In example with MATH we discarded fractional part as distance between adjecent symbols. This logic works for generalized integer. Number 74 is more than 58 but less than 100, so it is identified as 58. The range between adjacent numbers in alphabet is different but the method of extracting symbols from the whole number is the same. When symbol is identified it is excluded by removing correspondent row and column from our RANCOD pyramid. In this example it is subtraction 58*10010 and division by 42. Next step is performed in the same way with the same result of elimination next row and column from RANCOD and so on until the last symbol.
Based on this elementary example I see the range coder as generalization of base presentation of a number i.e. moving further from classical concept of base presentation like it was done when negative, irrational, complex numbers or fuzzy sets were introduced.
Numerical implementation
Formula (2) exists in more convenient iterative form
Mi = Mi-1 * n + Pi-1 * Ci
Pi = Pi-1 * Fi
where index i starts from 1, P0=1, M0 = 0. The computations according to iterative formula looks a little different but with same result
| # | symbol | f | C | Message |
| 0 | N | 42 | 58 | 58 |
| 1 | M | 27 | 31 | 58*100 + 42*31 = 7102 |
| 2 | L | 21 | 10 | 7102*100 + 42*27*10 = 721540 |
| 3 | N | 42 | 58 | 721540*100 + 42*27*21*58 = 73535212 |
| 4 | N | 42 | 58 | 73535212*100 + 42*27*21*42*58 = 7411532104 |
| 5 | N | 42 | 58 | 7411532104*100 + 42*27*21*42*42*58 = 743589668368 |
| 6 | K | 10 | 0 | 743589668368*100 + 42*27*21*42*42*42*0 = 74358966836800 |
| 7 | K | 10 | 0 | 74358966836800*100 + 42*27*21*42*42*42*10*0 = 7435896683680000 |
| 8 | N | 42 | 58 | 7435896683680000*100 + 42*27*21*42*42*42*10*10*58 = 743599901491465600 |
| 9 | M | 27 | 31 | 743599901491465600*100 + 42*27*21*42*42*42*10*10*42*31 = 74360219865125046400 |
| 10 | L | 21 | 10 | 74360219865125046400*100 + 42*27*21*42*42*42*10*10*42*27*10 = 7436023987264575328000 |
The programming challenge is clear from the last table. It is multiplication by denominator 100 and long products. First problem is easy. We adjust frequencies in order to make denominator to be power of 2. For example, multiply them all by 1.28. In this case multiplication by 128 will turn into binary shift. The computation of the product of frequencies can not be solved so easy. The solution is to keep certain portion of most significant bits as exact number and set the remained part to zero. The implementation can be clear from the function that performs this operation. The code is written for better understanding not for best performance.
long long SafeProduct(long long x, long long y, int mask, int& shift) {
long long p = x * y;
shift = 0;
while (p > mask) {
p >>= 1;
shift++;
}
return p;
}
The mask is an integer with all positive bits like 1111111. Function returns product and shift, which is the size of tail of zeros, used for the correct positioning of the product. In the chain of multiplication of frequencies the result will be an integer of constant bit length and shift can be accumulated producing the compression result. The remained part is correct positioning of all products adding them together and outputting bits. When all multiplications are done the addends represent numbers with long tails of zeros. When they are positioned after multiplication they form stair looking structure like follows
345678
56780091
8998111
661102
No matter how long is the message adding numbers at the tail do not affect beginning of the message, which is stable and can be output before operations are completed. The operations are conducted in 64 bit memory buffer that we call here 'Message'.
//Encoding
Message = 0;
Freqs = 1;
shift = 0;
for (int i=0; i < Size; i++) {
setBits(Message, base-shift);
Message <<= (base - shift);
Message += ((long long)(c[value[i]]) * Freqs);
Freqs = SafeProduct(Freqs, f[value[i]], Mask, shift);
}
setBits(Message, 64);
//Decoding
Freqs = 1;
shift = 0;
MSG = 0;
for (int i=0; i < Size; i++) {
MSG = getBits(MSG, base-shift);
ID = MSG/Freqs;
if ((symbol[ID]) != (value[i])) {
//error
break;
}
MSG -= Freqs*((long long)(c[symbol[ID]]));
Freqs = SafeProduct(Freqs, f[symbol[ID]], Mask, shift);
}
The addition of two integers can theoretically cause the buffer overflow. Since the size of
addend 'c[value[i]] * Freqs' is chosen much smaller than 'Message' and all high order bits in
'Message' are random the buffer overflow is very low probable and the problem can be ignored when
reliability of decoding is not mandatory for all data. Such cases as video compression,
for example, when failure to decompress couple of frames in two hours movie is allowed in
exchange of high encoding/decoding speed. For reliable decoding procedure the buffer
overflow problem has to be addressed.Co-contributer Bill Dorsey, whose help is very appreciated, investigated numerical stability and found few independent data samples where head of 'Message' accumulated certain number of positive bits causing buffer overflow and therefore failure in decoding. In a cooperative work we found a solution, making encoding/decoding reliable by additional operation. The concept is to normalize symbols to vary from 1 to maximum - minimum + 1 instead of [0, max-min] and reserve zero symbol as a special flag that is excluded from decoded stream and serve for the purpose of synchronization in encoding/decoding and also as a means of simple output of dangerously congested positive bits. This output is performed because c[0]=0 and f[0]=1, so function SafeProduct returns shift=0 and top base bits of 'Message' is output on the next step. The implementation details can be seen in self-test round trip program RanCode.cpp. Since final version is optimized for performance and have not very readable code we provide also an intermediate version that serves the purpose of better understanding of generic concept. The intermediate version does not have buffer overflow protection.
Patent situation
The developers of range coders like to repeat that opposite to arithmetic encoder the range coder is patent free, referring to Martins publication in 1979. U.S. pat 5,818,369 is range coder but it is dramatically different from Martins publication. The patented method is optimized performance achieved by look up tables that replace mathematical operations. It designed for small (preferably dual) alphabets, while suggested in this paper encoder works without adjustment for alphabets from 2 two 20000 and can be adjusted even for larger alphabets. Same principal difference can be pointed out by comparing it to known Q-coder (U.S. Pat. 4286256, 4463342, 4467317) and many other patents. There is known opinion of many programmers that software patents only increase entropy of our social system and should be abolished. Along with patentophobian programmers there are some others who publish arithmetic and range encoders on-line for a long time, FastAC, for example. It is called arithmetic encoder by author, but according to design it is closer to range encoder and has similarity with suggested in this paper range coder. Those who want to compare and benchmark these two encoders are very welcome.
Typically, infringement occurs when all elements of the main or broadest claim are presented in questioned device [6], [7]. We say 'typically', because other cases, when device simply considered as equivalent may also constitute an infringement. Anyway, it must be a great similarity between patented and questioned devices.
The strong line of defense for designers of range coders is not only Martins publication but also article of Mr. Langdon [4]. Langdon paper is published in a special journal that has reputation of defensive publications by IBM, which means publications for preventing others from patenting published materials. Langdon paper has explicit name and mentioned Martins coder which makes it recognized prior art reference by the expert of the industry. The encoder suggested in this paper is so close matching Martins paper that could be written next day after its publication. It can be also subjected to optimization by expediting arithmetical operations via hardware. Opposite to other patented approaches it requires standard multiplication and division tool only that means that performance optimization coprocessor can be chosen among available standard hardware.
Definition of entropy encoder
As it was shown in this paper range encoder is generalization of base presentation of the whole number that is regarded as property of nature introduced in implicit form together with Arabic numbers. The range coder is derived from arithmetic coder by such simple action as bringing involved fractions to common denominator. Arithmetic encoder acquired its name because of arithmetic operations required for encoding and decoding not because of the fractions and probabilities. Analytically both arithmetic and range encoders compute ranges and provide compression by choosing number between computed ranges either by reduction of fraction or by expressing integer with longest possible exponent that can be saved in more compact form. The length of encoded message is determined by statistical distribution of data and not by positioning of the symbols within the message. When the length of the message is large enough the size of encoded message equal to the size of number of possible permutations of symbols.
Based on these conclusive statements the following is suggested as definition of entropy encoder:
Entropy Encoding is a technique of reversible conversion of the message to a whole number, length of which is determined exclusively by statistical distribution of symbols and, with growing size of the message, numerically tends to the length of the number of possible permutations.
Acknowledgements
I wish to thank Michael Schiendler from Compression Consulting for very useful on-line discussion regarding stability and prevention of buffer overflow in suggested algorithm.
I also appreciate precious comments sent me by Dr. Paul E. Black who drew my attention to one logical imprecision in explanation that was immediately corrected.
Stephen Sarakas sent an important comment regarding patent law, very appreciated.
Bill Dorsey is cocontributor in solution of buffer overflow problem.
The comments are wellcome
andrewpolar@bellsouth.net
References
[1] C.E. Shannon, A mathematical theory of communications, Bell Syst. Tech. J., vol. 27, pp.379-423, July 1948.
[2] R. Pasco, Source Coding Algorithms for Fast Data Compression, Ph.D. Thesis, Department of Electrical Engineering, Stanford University, Stanford, CA, 1976.
[3] G.N.N. Martin, Range encoding: an algorithm for removing redundancy from digitized message. March 1979, Video & Data Recording Conference, Southampton, UK.
[4] Glen G. Langdon, An Introduction to Arithmetic Coding. IBM J. Res.Develop. Vol. 28, No. 2, March 1984.
[5] J. Rissanen, Arithmetic coding as number representations, Acta Poly-. tec, Scand., vol. 31, pp. 44-51, 1979
[6] David Pressman. Patent It Yourself. 11th edition. April 2005, Consolidated Printers, Inc.
[7] Richard Stim. Patent, Copyright and Trademark. January 2006, Consolidated Printers, Inc.
[8] Rissanen J.J. Generalized Kraft Inequality and Arithmetic Coding. IBM J.Res.Dev. May 1976, 198-203.
Copywrite (c) Andrew Polar. First publishing Feb. 3, 2007, but some corrections have been done later.
Topic 'Entropy revisited' is added on Apr. 28, 2007.
Topic 'Definition of entropy encoder' is edited on July 03, 2007
Topic 'Numerical implementation' is edited on August 19, 2007
The source code and theoretical approach is disclosed as prior art at IP.com (publication identifier IPCOM000144439D).
The paper article is published in 'The IP.com Journal'.