(Method is patented in U.S. 7315266, currently in public domain)
The compression of high quality photographic images is performed based on similarities in rows, columns, colors or separated repeated fragments. There is, however, one more correlation that is slipped out of attention or researchers. It is correlation between high order bits and low order bits within RGB structure. This correlation exists not in every image but in many of them, for example in known published 24 Kodak images used by many companies for compression benchmarks ( bitjazz , for example). This correlation is so strong that image palette can be used as look up table for prediction of low order bits based on high order counter part and low order bits can be compressed separately and independently from high order bits. This leads to possibility of improvement of any existing algorithm by excluding low order bits and processing them separately. The details along with code sample can be found in this article.
Table 2. below contains the comparison of compression ratios with and without separate processing of low order bits. The images are compressed by the method close to one published in article of S.A. Martucci 'Reversible compression of HDTV images using median adaptive prediction and arithmetic coding' in Proceedings of IEEE ISCAS, May 1990, pp. 1310-1313. The ratios are shown in coupled figures as 2.26/2.69. The number shown on the top 2.26 is compression ratio when only mentioned above method is applied. The number below 2.69 is compression ratio achieved when same algorithm was used along with suggested technique of separate processing of low order bits. Average improvement is about 18 percent. Both methods are lossless. Establishing a record was not an objective. The goal was to compare results for separate processing of low order bits, because the same technique can be used along with other, possibly, more effective methods (wavelet transforms, for example). Some comparison to other software is shown in table 1. The number in the table is total size of all 24 files when compression is applied separately to each of them. All original images are 768 * 512 RGB (that is 28,311,552 bytes). The list of companies is limited to those whose programs are easy available for test. It is not even close to some sort of exhaustive set and there are other companies and software versions that claim better compression but not freely available for testing or need significant time to install and test. To avoid misleading of visitors I have to add that very impressive compression by PAQ8P achieved for very long time such as about 36 seconds per image, while all other programs did it for sort of reasonable time between 1 and 3 sec.
| Method | Martucci 1990 | JPEG2000 | WinRK 2.1.6 | This article | HD Photo | PAQ8P | BMF v.1.1 Option -F |
| Reference | IEEE ISCAS | Luratech | WinRK | this method | dpktools.zip | PAQ8P | BMF |
| Size | 12,005,203 | 11,327,776 | 11,945,646 | 10,196,432 | 12,855,465 | 8,281,918 | 10,992,592 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
In the known algorithms lossless compression of still images is based on similarities between pixels in adjacent rows and columns also based on correlation between colors and similar fragment detected in different parts or image (LZ77, for example). One correlation in image data, however, slipped out of attention of researches. It is correlation between high order bits and low order bits within the same pixel. Surprisingly, in images not subjected to lossy compression the low order bits do not vary within theoretically possible limit but staying 'attached' to its high order counter part of RGB triplet. That means that knowledge of high order bits or RGB triplet can be used for successful statistical prediction of its low order counter part, using look up table. The benefits of such approach can be seen from statistical data shown in table 1. The data are taken for Kodak high quality photographic pictures that are in public domain and used by many researchers and companies for testing of compression algorithms (bitjazz, for example). Second column has image name used in original download site. Third column has size of palette for RGB triplets where last bit of every color is ignored. Fourth column has size of palette for full 24 bit triplets and the last column contains number of pixels.
Table 1. Statistical characteristics of Kodak images
| # | Image name | 21 bit palette | 24 bit palette | Number of pixels |
|---|---|---|---|---|
| 1 | Kodim01 | 17654 | 19182 | 393216 |
| 2 | Kodim02 | 12351 | 13452 | 393216 |
| 3 | Kodim03 | 31342 | 34871 | 393216 |
| 4 | Kodim04 | 29219 | 31716 | 393216 |
| 5 | Kodim05 | 58620 | 63558 | 393216 |
| 6 | Kodim06 | 23933 | 25964 | 393216 |
| 7 | Kodim07 | 34741 | 37552 | 393216 |
| 8 | Kodim08 | 41067 | 45558 | 393216 |
| 9 | Kodim09 | 22715 | 24106 | 393216 |
| 10 | Kodim10 | 20003 | 21537 | 393216 |
| 11 | Kodim11 | 31680 | 34473 | 393216 |
| 12 | Kodim12 | 23420 | 25567 | 393216 |
| 13 | Kodim13 | 35989 | 39784 | 393216 |
| 14 | Kodim14 | 51187 | 55117 | 393216 |
| 15 | Kodim15 | 41128 | 44576 | 393216 |
| 16 | Kodim16 | 13002 | 14096 | 393216 |
| 17 | Kodim17 | 18221 | 19815 | 393216 |
| 18 | Kodim18 | 52442 | 57415 | 393216 |
| 19 | Kodim19 | 22569 | 24807 | 393216 |
| 20 | Kodim20 | 22173 | 24470 | 393216 |
| 21 | Kodim21 | 26707 | 29317 | 393216 |
| 22 | Kodim22 | 47722 | 53351 | 393216 |
| 23 | Kodim23 | 65891 | 72079 | 393216 |
| 24 | Kodim24 | 38545 | 42351 | 393216 |
In some technical papers low order bits are called high frequency bits because they believed to be varied in full theoretical range in unpredicted way. This is true for images after JPEG transformation and not necessarily for raw data returned by light sensors. For full range theoretical variety of last three bits the difference between 21 bit palette and 24 bit palette should be near factor of 8. The actual difference is about 10 to 20 percent that means that most 21 bit fragments have unique 3 bit counter part in the image. If we use full 24 bit palette as look up table we can predict least significant bits using relative sequential index shown in table 2.
Table 2. Relative sequential index for low order bits in palette array
| High order bits | Low order bits | Relative sequential index | ||
|---|---|---|---|---|
| Red | Green | Blue | ||
| 1100001 | 1000111 | 1111000 | 101 | 0 |
| 1100001 | 1000111 | 1111000 | 110 | 1 |
| 1100001 | 1000111 | 1111000 | 111 | 2 |
| 1110010 | 0000011 | 1111001 | 001 | 0 |
In the table 24 bit RGB structure is split into 2 groups: high order bits that are 7 most significant bits of every color and low order group that is composed from 8th bit of every color. First 3 lines have identical high order group and different low order bits. We introduce relative sequential index for them 0,1 and 2. The 4th row in the table made new high order group so we start new relative sequential index starting from 0 and so on. According to observation made from the first table the relative sequential index for the whole palette contains approximately 80 percent of zeros and is expected be very well compressed by entropy encoder. High order bits may be compressed separately and independently from low order bits. In high order bit compression algorithm the last bit may be simply ignored or shifted out that significantly improves correlation between rows, columns and colors. There is, however, additional data that must be saved in order to restore original image without losses. It is palette fragment for low order bits (4th column in table 2) and special one bit mapping indicator the usage of which is explained further.
When high order bits are losslessly compressed and then restored, they form sorted 21 bit palette. In the table 2 this part is only two rows with different high order bit expressions like it is shown further in table 3.
Table 3. High order bit palette
| Red | Green | Blue |
|---|---|---|
| 1100001 | 1000111 | 1111000 |
| 1110010 | 0000011 | 1111001 |
The relative sequential index is compressed and restored as two dimensional array of data where every index value is located in the row and column of correspondent RGB triplet. When we restore original data we know, for example, first line from table 3 and relative sequential index 2. We need to make match between table 3 and 2. This is achieved by saving whole low order bit column with mapping indicator as it is shown in table 4.
Table 4. Mapping indicator
| Low order bits | Mapping indicator |
|---|---|
| 101 | 0 |
| 110 | 1 |
| 111 | 1 |
| 001 | 0 |
Mapping indicator is positive bit for the row where we need to repeat high order bit fragment and zero otherwise. Both tables 4 and 3 can be used to restore whole palette as it is shown in table 2. In order to do that 2 lines from table 3 are attached to 2 lines from table 4 where mapping indicator is 0 and repeated down in the lines where mapping indicator is 1. Obviously, we do not need to save 21 bit palette. It can be recreated when high order bits are decompressed. Losslessly compressed high order bits and relative sequential indexes along with low order bit part of palette and mapping indicator allow restore original image.
The compression ratio, obviously, depends on relation between 24 bit palette and image size and also on the ratio between 24 bit palette and 21 bit palette. For the considered sample of Kodak images these relations are in favor of compression of low order bits separately from high order bits. The ratios are slightly vary from image to image but we can show typical numbers. The average palette size is about 35,000. The image size is same for all 768 * 512. The relative ratio between 21 bit palette and 24 bit palette is about 1.09 that means that two dimensional array of relative sequential indexes may contains near 90 percent of zeros and small integers (mostly ones) in other 10 percent of data. The uncompressed low order bits have size of 768 * 512 * 3 = 1,179,648. With certain degree of approximation we can presume that relative sequential indexes are compressed by entropy encoder to the size of 768 * 512 * [-0.9 * log (0.9) - 0.1 * log (0.1)] = 184,417 bits. The part of low order bits in palette array along with mapping indicator takes about 35000 * 4 = 140,000 bits. The compression ratio for low order bits only is expected to be about 1179648 / (184417 + 140000) = 3.6 times. This ratio is larger than typical compression ratio for this sample of images reported by some companies as a benchmark, which is between 2.5 and 3.0. The independent compression of low order bits have dual benefits: low order bits are compressed better than image in average and other part of the image have chances to be compressed much better due to increased correlation in data after low order bits are excluded. The last circumstance allows this reversible compression of low order bits to be used in combination with many other algorithms independently whether it is LZ77, LZW, median adaptive prediction or other.

That explains what the program is for. The testing steps are elementary. From tools choose Compress/Restore option and select any 24 bit BMP file for compression. The compressed file will have *.plr extension and same name by default.
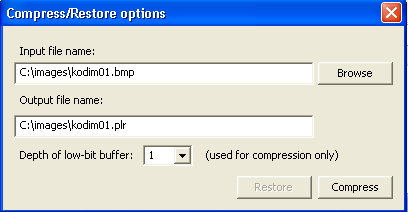
If file with extension *.plr is chosen program executes decompression. Original and restored files can be compared pixel by pixel to confirm lossless compression from other menu option. The input parameter 'Depth of low-bit-buffer' defines the size of low order bit fragment. Number 1 means that single least significant bit of every color will be taken to low order bit group, so the group size will be 3. When this size is chosen as 0 there is no low order bit group and compression is performed as shown in original article of Martucci. For Kodak images size 1 for bitdepth is optimal.
When compression completed the overall compression ratio is printed along with compression for low order bits.

Command line utility
Copyright (C) Andrew Polar. July 22, 2007.
Some language improvements were added on January 05, 2008.