Binary Arithmetic Coder
This article does not have scientific novelty and represents only educational materials for students and engineersIntroduction
As it is known arithmetic coding compress array of data very close to the size of the number of all possible permutations, which explains why compression has a theoretical limit. The process of compression is reduced to narrowing down the limits of chosen interval LOW and HIGH on every step, but the compression is achieved by choosing of the shortest fraction x between two finally computed limits LOW and HIGHLOW = C0 + C1 * P0 + C2 * P0 * P1 + C3 * P0 * P1 * P2+...
HIGH = LOW + P0 * P1 * P2 * P3+ ...
LOW <= x < HIGH
where Ci are cumulative probabilities and Pi are the probabilities of involved symbols. As it can be seen each encoding step requires at least two multiplications and decoding requires also one division along with these two multiplications. The details can be seen in implementation of RunCoder15, where long products of all probabilities are computed as MANTISSA and SHIFT, which needs two multiplications. Similar concept is employed in carryless coder, written by Subbotin, so it may be presumed that two multiplications can not be avoided on every step.
However, in 2002 Matt Mahoney wrote very tricky binary arithmetic coder (PAQ1) that requires only one multiplication per encoding and decoding step. There is an explanation in his original article but there is no match between the generic formula shown above and his algorithm. Also, there is a reasonable question: if it is possible to write binary arithmetic coder with one multiplication, may be it is also possible to write generic arithmetic or range coder with one multiplication per step.
Why binary coder?
Non-binary coders use two multiplications per step but each step compresses 8 bits at once. So they are more computationally effective than binary coders, why we use binary coders? There is one common problem for non-binary coders: they need to know the alphabet prior to encoding. We can make coder adaptive and adjust probabilities, but we have to know the size of the alphabet. Also, even when the size of the alphabet is known, it is necessary to make sort of dictionary for mapping symbols to indexes, because coder use indexes like 0,1,2,3,... instead of actual symbols. All these problems disappear in binary coders. If our symbols are large numbers we apply adaptive coding, where each symbol is coded bit by bit and lower bits are very well predicted for known upper bits, providing compression near the same limit as for large alphabet range coder. Binary coder can be applied in the same way and with the same efficiency to text files (with near 30 symbols) and to executables that employ all 256 bytes. Another advantage of binary coder is higher predictability for every single bit compared to bytes. For example, according to my observation most predictable bit in many computer files is the second bit in byte. It can be predicted with probability near 95 percent. Such information can not be used in adaptive range coders, where prediction is made for the whole byte? Certainly both range and binary coders should exist and most effective one should be chosen for the particular data type.PAQ version of binary coder
In binary version only two probabilities are available P0 = P{0} and P1 = P{1}. The encoding is started from dividing interval [0,1) in proportion of estimated probabilities and choosing left or right part of interval depending on occurred bit. Presume the first bit is 0 therefore the left segment must be chosen as it is marked in the picture below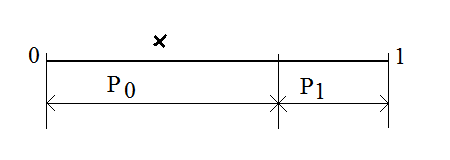
The example of codding the short sequence 0,1,0,1 is shown in the picture below.
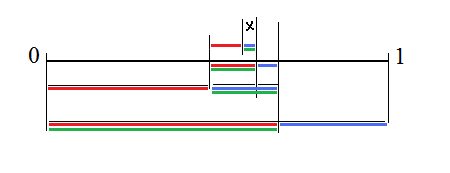
On the second step the chosen left interval is split in the same proportion and the right interval is chosen because the bit is 1. On the third step the interval is split again and left interval is chosen, and so on. The divided intervals are shown in the different colors: red is proportional to P0 and blue is proportional to P1. Green color marks the interval chosen according to the bit. At the end of encoding process any particular fraction from chosen interval (it is marked as x) may be selected. The reduction in size is occurred because the shortest fraction can be selected. In decoding the same split is performed and it is determined on which side of interval value x is located. If it is sitting to the left 0 bit is output and if to the right posititive bit is output. This algorithm is sitting in foundation of all PAQ compressors. Mathematically, for two borders x1 and x2 the mid point is computed as mid = (x2 - x1) * P1, and either right or left border is moved to mid by operation if (bit) x2 = mid; else x1 = mid. So the borders are narrowed on every step by only one multiplication.
Theoretical match
Mahoney algorithm can be interpreted as computation of new interval on each step as new left border and range. Obviously, range equals to product of all involved probabilities and match difference HIGH-LOW for theoretical formula. Let us compare left border to value of LOW limit. In the formula shown above indexes are sequential positions of symbols. If we replace them by concrete values C[0], C[1], P[0], P[1] for our fragment 0,1,0,1 we get expression like follows:LOW = C[0] + C[1] * P[0] + C[0] * P[0] * P[1] + C[1] * P[0] * P[1] * P[0]
Provided that C[0] = 0 and C[1] = P[0] we convert last expression into following:
LOW = P[0] * P[0] + P[0] * P[0] * P[1] * P[0]
and can see the match. Left border is sum of two fragments, which are calculated in accordance with last expression. The advantage of algorithm obviosly achieved only by particular values of cumulative probabilities. The generic algorithm should include computation of left border and range or left border and right border that requires two multiplications.
Binary coders
Those who want to see the actual PAQ coders may Google PAQ keyword and follow the links. I offered very simple example with reduced modeling part that can be easily comprehended by beginners before to move to not simple implementation of PAQ. This coder is actually written by Ilia Muraviev in his BALZ compressor. I extracted only elementary probability modeling part and arithmetic coder and made some insignificant changes. The arithmetic coder, shown in the program, in turn, extracted by Muraviev from Mahoney FPAQ1. Although the code is simple and shown for educational purpose it still provide relatively good compression not very far from best known industry coders, while being pretty quick and short. FPAQ coders are better due to better probability modeling. The higher is precision in predicting probability the higher is compression ratio.Using same concept for classic range coder
The same concept can be used for making range coder for larger alphabets. I wrote one experimental range coder based on the same concept, it is called Range Mapper . Since it is not binary coder it computes new ranges in encoding LEFT and RIGHT, so two multiplications is required. The upper bits are output, when they are identical. It is arranged in the same way as in Mahoney binary coder. However, LEFT and RIGHT boundaries sometimes becoming dangerously close and computation may collapse. One real example:| LEFT = | 1010100 11111111 11111111 11110100 |
| RIGHT = | 1010101 00000000 00000000 01010001 |
It can be seen that upper 8 bits are different and no output occur but the difference between RIGHT and LEFT is only 93. Next step in encoding lead to lost of precision and wrong result in decoding. In order to avoid this problem I simply output whole LOW or LEFT integer and set fresh new LOW = 0 and HIGH = 0xffffffff. That happens relatively rare so it does not make noticeable difference in compressed size. This coding concept is good for small alphabets. Larger alphabets need switch to 64 bit LOW and HIGH limits.
Andrew Polar, October, 2010.